Projects

Gradient Optimizing Chaogates

• Anil Radhakrishnan, Sudeshna Sinha, K. Murali, and William L. Ditto. (2025) “Gradient based optimization of Chaogates.” Chaos, Solitons & Fractals
  Github Published

Overview:

Chaogates represent a class of reconfigurable logic gates that leverage nonlinear maps for computation. While traditionally difficult to configure due to their high-dimensional parameter space and the non-differentiability of Boolean logic, this work introduces a differentiable formulation that enables gradient-based optimization.

Through this approach, each chaogate functions akin to a small neural network, achieving:

• Efficient Parameter Optimization: Simplifying the tuning of chaogates using machine learning techniques.
• Low Computational Overhead: Eliminating the need for high-parameter-count neural networks.

This opens avenues for automating parameter discovery in nonlinear computational devices and integrating chaogates into modern computation frameworks.

Chaogate Optimization Schematic

Technical Implementation:

• Frameworks: Built in Python using JAX with the Equinox Neural Network Library.
• Key Concepts: Gradient-Based Optimization, Nonlinear Dynamics, Differentiable Programming, Neural Networks.

Highlights:

• Simplified optimization: Leveraging machine learning techniques to efficiently tune chaogate parameters.
• Integration potential: Automating parameter discovery for use in modern computational frameworks.
• Bridging the gap: Connecting nonlinear systems with conventional neural network optimization.

Growing Neural Networks

• Anil Radhakrishnan, John F. Lindner, Scott T. Miller, Sudeshna Sinha, and William L. Ditto. (2025) “When less is more: evolving large neural networks from small ones.” arXiV
  Preprint Github

Current Status:

• Commercialization and Peer Review: Ongoing.

Overview:

This work explores a novel concept in artificial neural networks: Multi-Layer Perceptrons (MLPs) that dynamically grow their structure during training. Unlike conventional neural networks with fixed architectures, this approach enables adaptable networks that optimize both structure and performance as they learn.

Controller-Mask Algorithm Schematic

Technical Implementation:

• Frameworks: Built in Python using JAX with the Equinox Neural Network Library, prototyped in Mathematica.
• Key Concepts: Neural Networks, Gradient-based Optimization, AutoML, Network Theory.

Highlights:

• Dynamic Graph Learning: Adapting backpropagation to work on graphs with changing structures.
• Two Growth Perspectives:
  • Architecture Augmentation: Introducing a single auxiliary neuron to regulate network size.
  • Optimization Augmentation: Using a controller-mask mechanism to dynamically hide neurons during optimization with minimal overhead
• Structural learning curves: Extending the concept of learning rate curves to the structure of neural networks.

Metalearning Neural Activation Functions

• Anshul Choudhary, Anil Radhakrishnan, John F. Lindner, Sudeshna Sinha, and William L. Ditto. (2023) “Neural networks embrace learned diversity.” Nature Scientific Reports
  Preprint Github Published
• Kathleen Marie Russel, William L. Ditto, Anshul Choudhary, Anil Radhakrishnan, and John F. Lindner. (2023) “Diversity Based Deep Learning System.”
  Patent Pending Published

Overview:

This project explores an approach where neural networks learn their own activation functions dynamically during training. Instead of relying on fixed or predefined activations, activation functions are represented as neural subnetworks that adaptively optimize 1-1 nonlinear mappings in situ while the main network simultaneously learns the task at hand.

Metalearning Activations Schematic

Technical Implementation:

• Frameworks: Initial implementation in Python using PyTorch, additional experiments in JAX with the Equinox Neural Network Library.
• Key Concepts: Neural Networks, Metalearning, Physics informed Neural Networks, Introspection

Highlights:

• Activation Subnetworks: Each class of activation functions is represented by a neural subnetwork that learns alongside the main network.
• Meta-Learning Framework: Activation functions are optimized simultaneously with the primary network, enabling dynamic task-specific adaptations.
• Versatility: Demonstrates wide applicability across domains such as machine learning, time-series forecasting, and physics-informed modeling.
• Adaptability: Pioneers a new paradigm where neural networks autonomously design their activation strategies.

Neural Network Control of Chaos

Current Status:

• On Hiatus

Overview:

This project takes on the problem of controlling chaotic systems using neural networks. Realizing that full simulation of chaotic systems is computationally expensive and often infeasible, we develop neural network controllers based on neural ordinary differential equations that learn control signals that steer the dynamical systems towards the desired target state. Although these problems are theoretically formulable as optimal control problems within variational calculus the solutions are often intractable. We demonstrate that neural networks can learn to control chaotic systems with high accuracy and efficiency.

Neural Network Control Schematic

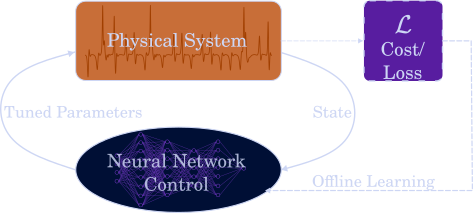
Technical Implementation:

• Frameworks: Built in Python using JAX with the Equinox Neural Network Library and Diffrax differential equation solver.
• Key Concepts: Neural ODEs, Nonlinear Dynamics, Chaos Theory, Optimal Control, Stochastic Differential Equations

Highlights:

• Synchronous phase-locked control: Demonstrated control of high-dimensional nonlinear pendulum array systems.
• Active control: Achieved control of noisy Kuramoto oscillators.
• Novel recurrence matrices: Used to specify control targets in high-dimensional systems.

Other things I’ve worked on

High Energy Physics

Leptons are elementary particles with half integer spins (like electrons) that are crucial in the study of high energy physics. Many times it is important to differentiate between leptons that are produced in the initial collision and those that are produced in the decay of other particles. We worked to develop a reccurent neural network-based model that can identify and isolate leptons from other particles in collision data from the ATLAS detector at CERN. All neural network models were built in Python using PyTorch.

Quantum Computing

I have experience with Qiskit, a quantum computing software development kit developed by IBM. I have also built classical quantum computer simulators in Julia and Python and have worked with quantum algorithms like Grover’s and Shor’s algorithms. I have also built quantum machine learning models like variational eigensolvers.

Condensed Matter Physics

I have worked with ultrafast laser systems to study magnetization dynamics in thin films. I have experience with lithography and thin film deposition techniques along with various characterization techniques like X-ray diffraction and atomic force microscopy.

I have worked on developing an optical second harmonic detection system to study antiferromagnetic thin films.

I have also characterized superconducting RF cavity dirty layers and their effect on cavity performance. To do so effectively, I developed simulations of Bardeen-Cooper-Schrieffer (BCS) theory and London theory to study the effect of dirty layers on superconducting properties, improving data analysis efficiency by 48 times due to reduced human intervention compared to previous methods.

Monte Carlo simulations

I have used classical and quantum Monte Carlo to create atomic scale simulations with the Lennard-Jones potential.